#7 phương pháp giải phương trình bậc 2 cực đơn giản

Hôm nay, chúng tôi sẽ chia sẻ với các bạn các cách giải phương trình bậc 2 một cách dễ dàng và hiệu quả. Hãy sẵn sàng lựa chọn nhé!

Định nghĩa phương trình bậc 2

Phương trình bậc hai có dạng ax²+bx+c=0, trong đó a khác 0.

Ví dụ: x²+2x-5=0 là một phương trình bậc hai.

Các cách giải phương trình bậc 2 cần nhớ

Tính biệt thức Delta

Đây là phương pháp phổ biến nhất và rất đơn giản để áp dụng. Bạn chỉ cần nhớ công thức là được.

Lời giải:

Tính biệt thức Delta‘

Phương pháp này thích hợp khi b là một số nguyên chẵn, tức là b = 2b’. Đây cũng là phương pháp tiện dụng khi các hệ số a, b, c có giá trị lớn.

Lời giải:

Hệ Quả Của Định Lý Viète

Phương pháp này giúp tiết kiệm thời gian và công sức trong việc giải bài tập, tuy nhiên áp dụng hạn chế trong thực tế.

Lời giải:

Nhẩm nghiệm giải phương trình bậc 2

Phương pháp đồ thị

Phương pháp này áp dụng cho phương trình bậc 2, 3 và 4 khi nghiệm là số nguyên và bạn có thể vẽ đồ thị của chúng.

Lời giải:

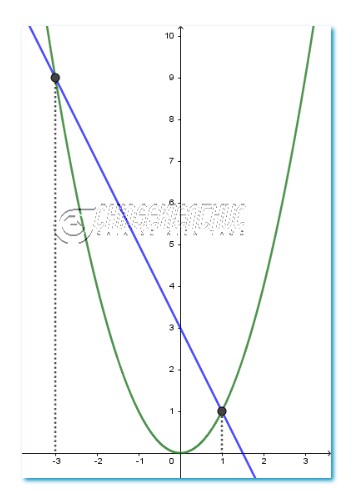
Phương trình đã cho tương đương với x²=-2x+3

Đặt f(x)=x² và g(x)=-2x+3 Vẽ f(x) và g(x) trên cùng một hệ trục tọa độ. Hoành độ giao điểm của đồ thị hàm số f(x) và g(x) chính là nghiệm của phương trình.

Quan sát đồ thị, ta thấy hoành độ của hai giao điểm lần lượt là 1 và -3. Do đó, ta có thể dự đoán 1 và -3 là 2 nghiệm của phương trình đã cho.

Thay 1 và -3 lần lượt vào phương trình đã cho, ta có (1)²+2(1)-3=0 và (-3)²+2(-3)-3=0 (thỏa mãn)

==> Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3.

Chú ý: 

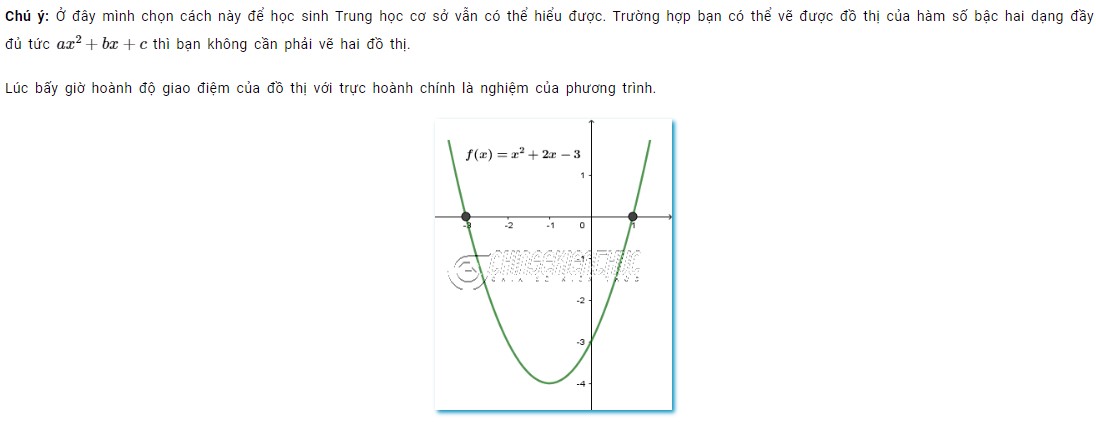
Phương pháp máy tính CASIO

Phương pháp này thích hợp để kiểm tra kết quả hoặc giải các bài kiểm tra/bài thi trắc nghiệm.

Lời Giải:

• Bước 1: Chọn phương thức tính toán Equation/Func
• Bước 2: Chọn Polynomial
• Bước 3: Chọn bậc 2 (vì chúng ta giải phương trình bậc 2)
• Bước 4: Nhập các hệ số …
• Bước 5: Nhấn phím = để thu được nghiệm thứ nhất, tiếp tục nhấn phím = để thu được nghiệm thứ 2 Nếu tiếp tục nhấn phím =, ta sẽ thu được hoành độ và trung độ của điểm cực tiểu.

Chú ý: Phương pháp này có thể tìm được nghiệm của phương trình bậc 2, 3 và 4.

Phương pháp biến đổi tổng quát

Phương pháp này giúp rèn luyện khả năng tư duy, tính toán và tìm nghiệm trong trường hợp tổng quát.

Lời giải:

• Xem thêm: Phương pháp giải phương trình bậc 4 đơn giản, dễ hiểu nhất

Trên đây là các cách giải phương trình bậc 2 mà chúng ta đã tổng hợp lại. Hãy linh hoạt áp dụng để tiết kiệm thời gian và làm bài tập hiệu quả hơn nhé! Hy vọng bài viết này hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại trong những bài viết tiếp theo trên kienthuconline24h.com!