Tìm hiểu về trực tâm tam giác và cách xác định toạ độ trực tâm tam giác

Trong bài viết này, chúng ta sẽ tìm hiểu cách tìm toạ độ trực tâm của tam giác và ứng dụng của nó trong đời sống. 

Trực tâm của tam giác là gì?

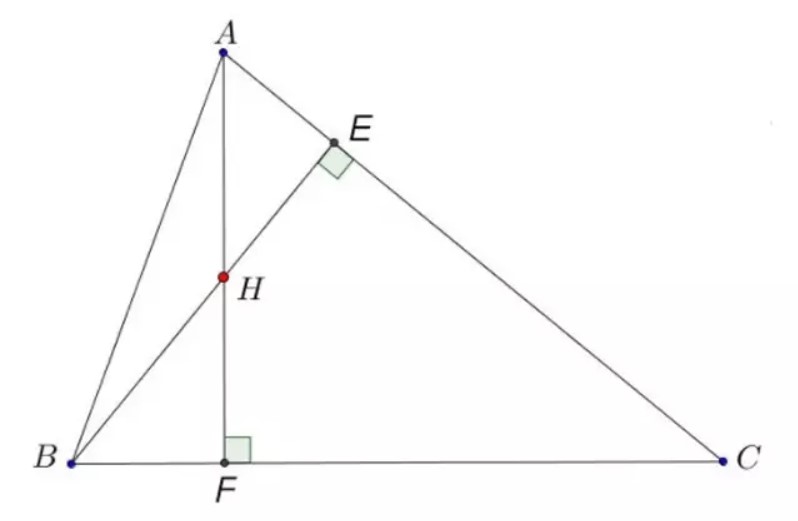
Trực tâm của tam giác là điểm giao nhau của ba đường cao trong tam giác đó. Đường cao là đường thẳng đi qua một đỉnh và vuông góc với cạnh tương ứng. Điểm trực tâm của tam giác cũng được xác định bằng cách kẻ hai đường cao trong tam giác.

Cách tìm toạ độ trực tâm của tam giác

Để tìm tọa độ trực tâm của tam giác, ta có thể kẻ hai đường cao tương ứng từ hai đỉnh khác nhau của tam giác. Điểm giao nhau của hai đường cao đó chính là tọa độ trực tâm của tam giác. Đối với tam giác vuông, tọa độ trực tâm trùng với giao điểm của hai cạnh vuông.

Tính chất của trực tâm của tam giác

• Tính chất 1: Trong tam giác cân, đường trung trực tương ứng cạnh đáy đồng thời là đường phân giác, đường trung tuyến và đường cao.
• Tính chất 2: Trong tam giác, nếu đường trung tuyến và đường phân giác trùng nhau, tam giác đó là tam giác cân.
• Tính chất 3: Trong tam giác, nếu đường trung tuyến và đường trung trực trùng nhau, tam giác đó là tam giác cân.
• Tính chất 4: Trong tam giác nhọn, trực tâm trùng với tâm của đường tròn nội tiếp có 3 đỉnh là chân của 3 đường cao đến các cạnh tương ứng.
• Tính chất 5: Nếu đường cao của tam giác cắt đường tròn ngoại tiếp tại hai điểm phân biệt, điểm thứ hai đối xứng với trực tâm qua cạnh tương ứng.

Một số bài tập vận dụng

Dưới đây là một số dạng bài tập để bạn tham khảo:

• Bài 1: Cho tam giác ABC có tọa độ tương ứng A(-2;6), B(-2;9), C(-4,7). Hãy tìm tọa độ trực tâm.
• Bài 2: Cho tam giác ABC có tọa độ tương ứng A(-1; 1), B(3; 1), C(2; 4). Hãy tìm tọa độ trực tâm.
• Bài 3: Cho tam giác ABC có tọa độ tương ứng A(5 ;4), B(2 ;7), C(-2 ;-1). Hãy tìm tọa độ trực tâm.

Ứng dụng của tọa độ trực tâm là gì?

Tọa độ trực tâm của tam giác có ứng dụng cao trong lĩnh vực đất đai và địa chất. Khi phân chia đất đai hoặc tìm kiếm trọng tâm của một khu đất hình tam giác, kiến thức về tọa độ trực tâm là rất hữu ích. Tuy nhiên, việc này cần sử dụng các thiết bị chuyên dụng để đảm bảo tính chính xác.

Hy vọng rằng với những kiến thức được cung cấp ở trên, bạn đã hiểu về cách tìm toạ độ trực tâm của tam giác và các tính chất liên quan. Hình học không gian được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, và nếu bạn quan tâm, hãy tìm hiểu thêm các kiến thức bổ ích trên website của Kiến thức online 24h nhé.