Các công thức tính hàm ngược và đạo hàm hàm ngược dễ nhớ nhất

Hàm ngược có ứng dụng rất lớn mà bạn không ngờ đến. Đôi lúc, chúng ta có thể áp dụng tính chất của hàm ngược để giải quyết những vấn đề phi toán học. Vậy hàm số ngược là gì mà lại hữu dụng đến vậy? Bài viết này sẽ giúp bạn hiểu khái niệm và cách tìm hàm ngược.

Hàm ngược là gì?

Hàm ngược, hay còn được gọi là hàm nghịch đảo, là một hàm mà biến đầu vào là kết quả của một hàm khác. Trong toán học, hàm ngược là việc hoàn tác lại những gì đã được tính toán của một hàm. Khi một hàm f có hàm nghịch đảo tương ứng, ta gọi hàm f là khả nghịch. Hàm nghịch đảo của hàm f được ký hiệu là f-1.

Điều kiện để hàm f khả nghịch là song ánh, tức là với mỗi giá trị x thuộc tập X, ta chỉ tìm được duy nhất một giá trị y tương ứng thuộc tập Y. Mối quan hệ này có thể được biểu diễn như sau: f(x) = y và f-1(y) = x. Trong đó, f(x) là hàm chứa biến x đã cho, còn f-1(y) là hàm nghịch đảo của hàm f(x) theo biến y. Từ mối quan hệ trên, hàm nghịch đảo của f(x) sẽ được biểu diễn ở dạng tổng quát như sau: f-1(y) = (phần tử duy nhất x ∊ X sao cho f(x) = y).

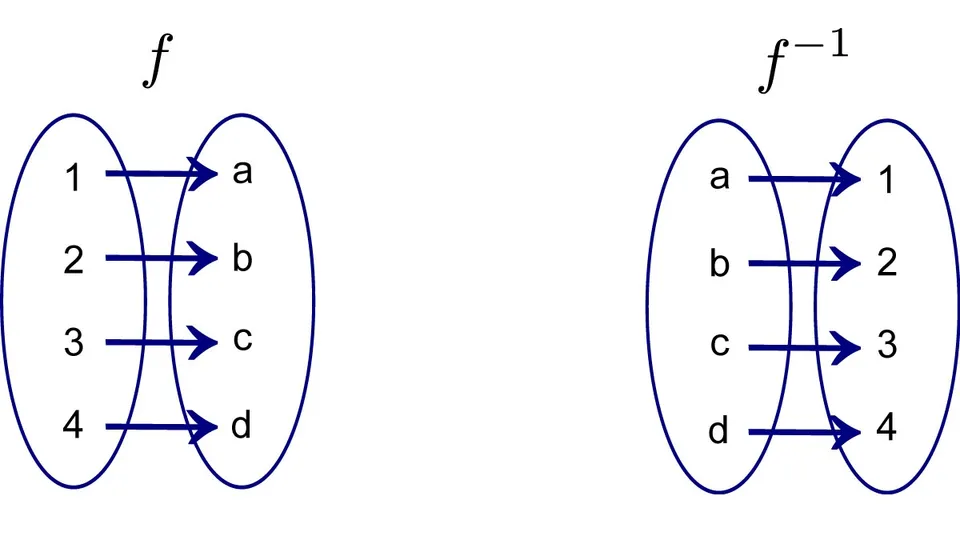
Công thức tính hàm ngược

Với một số hàm cơ bản như ex, 2x,…, việc tìm hàm nghịch đảo có thể mất nhiều thời gian. Để rút ngắn quá trình tính toán, bạn có thể tra bảng tương ứng để biết công thức hàm ngược. Để áp dụng cách tìm hàm ngược thành công, bạn cần chú ý đến phần điều kiện. Nếu hàm không thỏa điều kiện, chúng sẽ không khả nghịch.

Các ví dụ về hàm ngược cơ bản

Để giúp bạn hiểu rõ hơn về hàm nghịch đảo, hãy xem một số ví dụ cụ thể sau đây:

Hàm bậc nhất

Mỗi hàm bậc nhất luôn có một hàm nghịch đảo tương ứng, hay có thể nói mọi hàm bậc nhất đều khả nghịch. Xét ví dụ với hàm f(x) = 2x – 3. Khi đó, hàm nghịch đảo của f(x) = 2x – 3 là f-1(y) = (y + 3)/2.

Hàm bình phương

Mọi hàm bình phương đều không khả nghịch trên miền giá trị R. Để khả nghịch, bạn cần xét hàm bình phương trên khoảng giá trị không âm. Với hàm f(x) = x2 có miền giá trị [0,), hàm f-1(y) = y.

Cách tính đạo hàm hàm ngược

Trước khi tính đạo hàm của hàm nghịch đảo, bạn cần xét tính khả vi của hàm. Nếu hàm f khả vi trên khoảng A thì hàm nghịch đảo của hàm f, tức f-1, sẽ khả vi trên khoảng f(A). Theo định lý hàm ngược, đạo hàm của hàm này được tính theo công thức tổng quát: (f-1)'(y) = 1/(f'(x)).

Tính chất của hàm ngược

Hàm nghịch đảo có một số tính chất cơ bản dựa vào bản chất của hàm. Bạn có thể dựa vào chúng để áp dụng và giải các bài toán.

Tính duy nhất

Mỗi hàm f chỉ có duy nhất một hàm nghịch đảo f-1 tương ứng. Ngược lại, mỗi hàm f-1 cũng chỉ có duy nhất một hàm f tương ứng.

Tính đối xứng

Hàm f và hàm ngược của hàm f có tính đối xứng với nhau. Tính chất này thể hiện rõ nhất qua đồ thị của hai hàm trên hệ trục Oxy.

Theo đồ thị, mọi các cặp hàm f và f-1 đều đối xứng qua một trục, là đường thẳng y=x. Bên cạnh hàm bậc 1 và bậc 2, các hàm sơ cấp khác cũng có tính chất đối xứng này. Ngoài ra, hàm hợp cũng thể hiện tính chất này nhưng không thể hiện qua đồ thị của hàm. Thay vào đó, tính chất thể hiện thông qua cách tính toán theo phương pháp đại số. Hàm nghịch đảo của hàm hợp g°f là (g°f)-1= f-1 ºg-1. Với hàm hợp, khi tính toán, thứ tự tính các hàm sẽ bị thay đổi, cụ thể là g đổi chỗ với f.

Đồ thị của hàm ngược

Sau đây là đồ thị biểu diễn hàm nghịch đảo của hàm 2x:

Hàm tự nghịch đảo

Hàm tự nghịch đảo là hàm đồng nhất. Khi biểu diễn trên đồ thị, hàm tự nghịch đảo chính là trục đối xứng của chính nó và các hàm khác. Hàm y = x là một trong những hàm tự nghịch đảo đã được công bố.

Cách xử lý hàm ngược

Để tính toán hàm nghịch đảo, bạn cần áp dụng quy tắc và công thức. Dưới đây là các bước cơ bản để tính hàm ngược:

Các bước cơ bản để tính hàm ngược

• Bước 1: Đưa hàm đã cho về dạng y = f(x).
• Bước 2: Xét điều kiện song ánh của hàm f(x).
• Bước 3: Nếu thỏa điều kiện, biến đổi về dạng x = f(y).
• Bước 4: Kết luận.

Cách tìm hàm lượng giác nghịch đảo

Với hàm lượng giác nghịch đảo, bạn cũng làm theo các bước cơ bản nêu trên. Tuy nhiên, lưu ý các giá trị của hàm luôn nhỏ hơn 1 hoặc là dạng radian.

Các bài tập về hàm ngược có lời giải

Bài tập 1: Tìm hàm nghịch đảo của hàm f(x) = ln (x + 3)

Lời giải: Điều kiện x (-3;∞)

Ta có: ln (x + 3) = y ⇔ x + 3 = ey ⇔ x = ey – 3

Vậy hàm nghịch đảo của hàm f(x) = ln (x + 3) là f-1= ey – 3.

Bài tập 2: Cho f(x) = (3x + 2)/(x+1). Hãy tìm hàm nghịch đảo của hàm trên.

Lời giải: Điều kiện x ≠ -1

Ta có: (3x + 2)/(x+1) = y ⇔ 3x + 2 = y (x + 1) ⇔ 3x + 2 = yx + y ⇔ 3x – yx = y – 2 ⇔ x (3 – y) = y – 2 ⇔ x = (y – 2)/(3-y)

Vậy hàm nghịch đảo của hàm f(x) đã cho là f-1 = (y – 2)/(3-y).

Nói chung, cách tìm hàm ngược không chỉ có tính ứng dụng trong toán học mà còn trong các lĩnh vực khác. Lý thuyết và tính ứng dụng của loại hàm này đã được lồng ghép sẵn vào trong cách tính toán và những bài học cơ bản khác. Hãy theo dõi Kienthucobline24h để tìm hiểu thêm về những công thức toán học khác.