Bí quyết học thuộc các công thức lượng giác nhớ cực lâu

Khi nhắc đến môn toán, không thể không nhắc đến công thức lượng giác. Đây là một phần kiến thức vô cùng quan trọng trong kỳ thi THPT Quốc gia. Trong bài viết hôm nay, chúng ta sẽ cùng nhau tìm hiểu cách học thuộc công thức lượng giác, ôn lại các kiến thức liên quan đến góc và công thức lượng giác ngay sau đây.

Định nghĩa về góc lượng giác

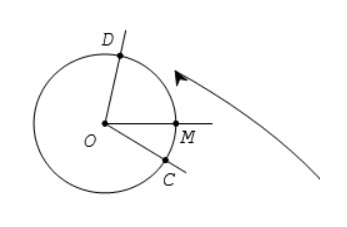
Trên đường tròn định hướng cho một cung lượng giác, một điểm M chuyển động trên đường tròn từ C tới D tạo nên cung lượng giác đó. Khi đó, tia OM quay xung quanh gốc O từ vị trí OC tới vị trí OD. Ta nói tia OM tạo ra một góc lượng giác, có tia đầu là OC và tia cuối là OD.

Kí hiệu của góc lượng giác là (OC, OD). Góc lượng giác còn được biểu diễn trên đường tròn lượng giác.

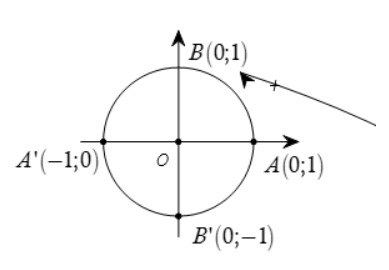
Ví dụ: Trong mặt phẳng tọa độ Oxy, vẽ đường tròn định hướng tâm O bán kính R = 1. Đường tròn này cắt hai trục tọa độ tại bốn điểm A(1; 0), A'(-1; 0); B(0; 1); B(0; -1). Ta lấy A(1; 0) làm điểm gốc của đường tròn đó. Đường tròn xác định như trên được gọi là đường tròn lượng giác (gốc A).

Công thức lượng giác đầy đủ nhất

Để có thể làm tốt bài tập về phần này, các bạn cần phải học thuộc những công thức sau. Sau đây là bảng công thức lượng giác đầy đủ bao gồm công thức lượng giác cơ bản và nâng cao.

Công thức lượng giác của các cung có liên hoàn đặc biệt

Cung đối nhau: α và -α

• cos(-α) = cosα
• sin(-α) = -sinα
• tan(-α) = -tanα
• cot(-α) = -cotα

Cung phụ nhau: α và π – α

• sin(π – α)= sinα
• cos(π – α)= -cosα
• tan(π – α)= -tanα
• cot(π – α)= -cotα

Cung hơn kém π: α và (α + π)

• sin(α + π) = -sinα
• cos(α + π) = -cosα
• tan(α + π) = tanα
• cot(α + π) = cotα

Cung phụ nhau: α và (π/2 – α)

• sin(π/2- α) = cosα
• cos(π/2- α) = sinα
• tan(π/2- α) = cotα
• cot(π/2- α) = tanα

Cung hơn kém nhau π/2:

• Cos(π/2+ x) = -sinx
• Sin(π/2+ x) = cosx
  Ghi chú: Cos đối, Sin bù, Phụ chéo hơn kém π là tan và cot.

Công thức lượng giác cơ bản

• Công thức lượng giác cơ bản:

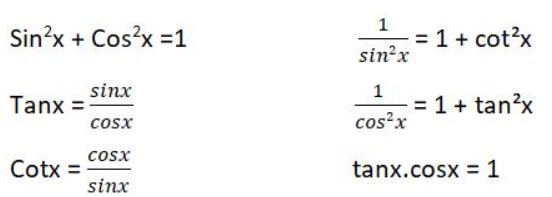
• Công thức cộng:
  
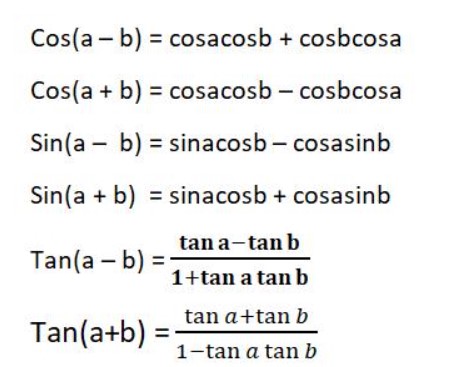
• Công thức nhân:
  
• Công thức hạ bậc:

• Công thức biến tổng thành tích:

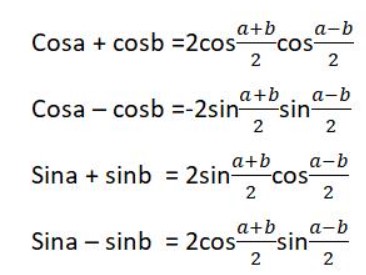
• Công thức biến tích thành tổng:

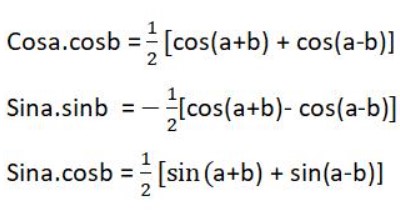
Công thức nghiệm của phương trình lượng giác cơ bản

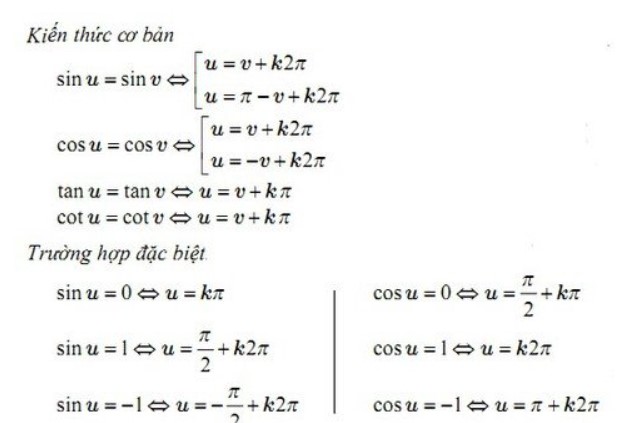
Cách học thuộc công thức lượng giác nhanh nhất

Do công thức lượng giác là những công thức rất khó để nhớ. Chúng ta có thể đọc thành thơ để hiểu hơn và nhớ bài một cách nhanh nhất như sau:

Bài thơ về công thức cộng lượng giác

Cos trừ cos = 2 cos cos

Cos trừ cos =-2 sin sin

Sin cộng sin = 2 sin cos

Sin trừ sin = 2 cos sin

Sin thì sin cos cos sin

Cos thì cos cos sin sin “coi chừng” (dấu trừ)

Tang tổng thì lấy tổng tang

Chia một trừ với tích tang

Bài thơ về công thức nhân ba

Nhân ba một góc bất kỳ,

Sin thì ba bốn, cos thì bốn ba,

Dấu trừ đặt giữa 2 ta, lập phương chỗ bốn.

Bài thơ về cách biến đổi tổng thành tích

Sin tổng lập tổng sin cô

Cô tổng lập hiệu đôi cô đôi chàng

Còn tan tử cộng đôi tan (hoặc là: tan tổng lập tổng 2 tan)

Một trừ tan tích mẫu mang thương sầu

Gặp hiệu ta chớ lo âu,

Đổi trừ thành cộng ghi sâu vào lòng.

Mẹo học công thức biến tích thành tổng

Cos cos nửa cos-+, + cos-trừ

Sin sin nửa cos-trừ trừ cos-+

Sin cos nửa sin-+ + sin-trừ

Cách nhớ công thức tan(a+b)=(tan+tanb)/1-tana.tanb

Tan một tổng 2 tầng cao rộng

Trên thượng tầng tan + tan tan

Dưới hạ tầng số 1 ngang tàng

Dám trừ một tích tan tan oai hùng

Cách thuộc giá trị lượng giác các cung đặc biệt

Cos đối, sin bù, phụ chéo, khác pi tan

Cosin của 2 góc đối bằng nhau; sin của 2 góc bù nhau thì bằng nhau;

phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tan góc này = cot góc kia;

tan của 2 góc hơn kém pi thì bằng nhau.

Cách học thuộc hàm số lượng giác

Cách 1:

Bắt được quả tang

Sin nằm trên cos (tan@ = sin@:cos@)

Cotang dại dột

Bị cos đè cho.

Cách 2:

Bắt được quả tang

Sin nằm trên cos

Côtang cãi lại

Cos nằm trên sin!

Như vậy qua bài viết hôm nay, chúng ta đã có thể nhớ lại và ôn tập về lý thuyết và cách học thuộc công thức lượng giác. Hi vọng với những kiến thức bổ ích này, sẽ giúp các em có thể ôn tập và rèn luyện lại kiến thức về lượng giác của mình một cách tốt nhất.