Tổng hợp 2 cách chứng minh trọng tâm trong tam giác dễ nhớ

Trọng tâm tam giác là một khái niệm quan trọng trong học từ lớp 7. Nhưng trọng tâm là gì? Cách chứng minh trọng tâm của tam giác như thế nào? Bài viết dưới đây sẽ giải đáp những câu hỏi đó cho bạn.

Định nghĩa trọng tâm tam giác

Trọng tâm của tam giác là giao điểm của ba đường trung tuyến của tam giác. Điều này được ghi lại trong sách giáo khoa: “Trong 1 tam giác có 3 đường trung tuyến. 3 đường trung tuyến này cùng đi qua một điểm, điểm này được gọi là trọng tâm của tam giác”.

Ví dụ: Tam giác ABC với ba đường trung tuyến AM, BN, CP cùng đi qua giao điểm G. G chính là trọng tâm của tam giác ABC.

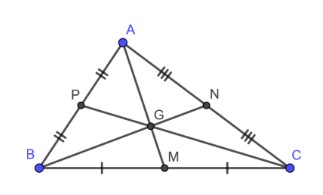
Tính chất trọng tâm tam giác

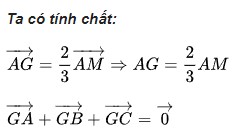
Tính chất của trọng tâm tam giác là: Khoảng cách từ trọng tâm tới 3 đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến tương ứng với đỉnh đó.

Ví dụ: Cho tam giác ABC có trọng tâm G và đường trung tuyến AM = 12cm. Tính độ dài đoạn AG và GM.

Cách chứng minh trọng tâm của tam giác

Có hai cách để xác định trọng tâm của một tam giác.

Cách 1:

• Tìm trung điểm M của BC sao cho MC = MB.
• Nối A với M ta được đường trung tuyến AM.
• Làm tương tự với các đường trung tuyến còn lại.
• Giao 3 đường trung tuyến là điểm G. Suy ra G chính là trọng tâm tam giác ABC.

Cách 2:

• Tìm trung điểm M của BC sao cho MC = MB.
• Nối A với M ta được đường trung tuyến AM.
• Trên đoạn thẳng AM lấy điểm G sao cho: AG = 2/3 AM
• Theo tính chất trọng tâm, G chính là trọng tâm tam giác ABC.

• Xem thêm: Cách tìm tọa độ trực tâm của tam giác nhanh nhất

Trọng tâm của các hình học đặc biệt

• Trọng tâm tam giác vuông: Tam giác ABC vuông tại B, từ B vẽ đường trung tuyến BA. Vì BA là đường trung tuyến của góc vuông nên: BA = 1/2 CD = AD = AC. Vậy tam giác ADB và tam giác ABC lần lượt cân tại A.

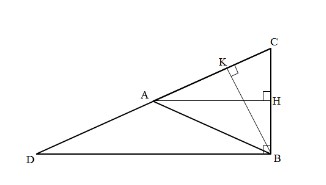
• Trọng tâm tam giác cân: Cho tam giác ABC cân tại A, G là trọng tâm tam giác ABC. Vì tam giác cân tại A, nên AG vừa là đường trung tuyến, vừa là đường cao và là đường phân giác của tam giác ABC.

• Trọng tâm tam giác đều: Cho tam giác ABC đều, G là giao điểm ba đường trung tuyến. Theo tính chất của tam giác đều ta có G vừa là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.

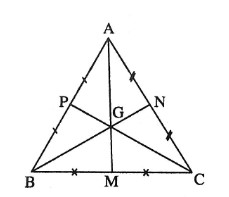
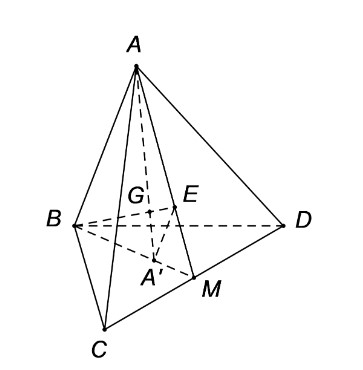
• Trọng tâm tứ diện: Trọng tâm tứ diện là giao điểm của bốn đường thẳng nối đỉnh và trọng tâm của tam giác đối diện.

Bài tập trọng tâm của tam giác

• Bài tập 1: Cho tam giác ABC, trung tuyến BM = CN. BM cắt CN tại G. Chứng minh tam giác ABC cân tại A.
• Bài tập 2: Cho I là trọng tâm của tam giác đều MNP. Chứng minh rằng: IM = IN = IP.
• Bài tập 3: Tam giác ABC có trung tuyến AD = 9cm và trọng tâm I. Tính độ dài đoạn AI.

Với kiến thức về trọng tâm tam giác và bài tập luyện tập, bạn sẽ nắm vững hơn trong việc giải quyết các bài tập hình học. Đừng quên truy cập kienthuconline24h.com để tìm hiểu thêm những thông tin bổ ích nhé!