Cách chứng minh đồng dạng của tam giác Đơn giản & Hiệu quả

Tam giác đồng dạng và cách chứng minh đồng dạng của tam giác là những kiến thức vô cùng quan trọng trong môn Toán lớp 8 phần Hình học. Trong bài viết này, chúng ta sẽ đi vào tìm hiểu về các trường hợp đồng dạng của tam giác và một số bài toán chứng minh tam giác đồng dạng.

Nhắc lại các trường hợp đồng dạng của tam giác

1.1. Các trường hợp đồng dạng của tam giác thường

• Cạnh – cạnh – cạnh (c.c.c)
• Cạnh – góc – cạnh (c.g.c)
• Góc – góc (g.g)

1.2. Các trường hợp đồng dạng của tam giác vuông

• Cạnh huyền – cạnh góc vuông
• Hai cạnh góc vuông
• Một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia

Để tìm hiểu chi tiết về tất cả các trường hợp đồng dạng tam giác, bạn hãy truy cập bài viết dưới đây để tham khảo nhé:

• Tổng hợp các trường hợp đồng dạng của tam giác cần ghi nhớ

Cách chứng minh đồng dạng của tam giác

2.1. Chứng minh tam giác đồng dạng một cách trực tiếp

Ví dụ: Cho tam giác ABC nhọn. Từ A kẻ AH vuông góc với BC (H BC), từ H kẻ HK vuông góc với AC (K AC). Chứng minh tam giác AHC đồng dạng với tam giác HKC.

Giải

Xét tam giác AHC và tam giác HKC có:

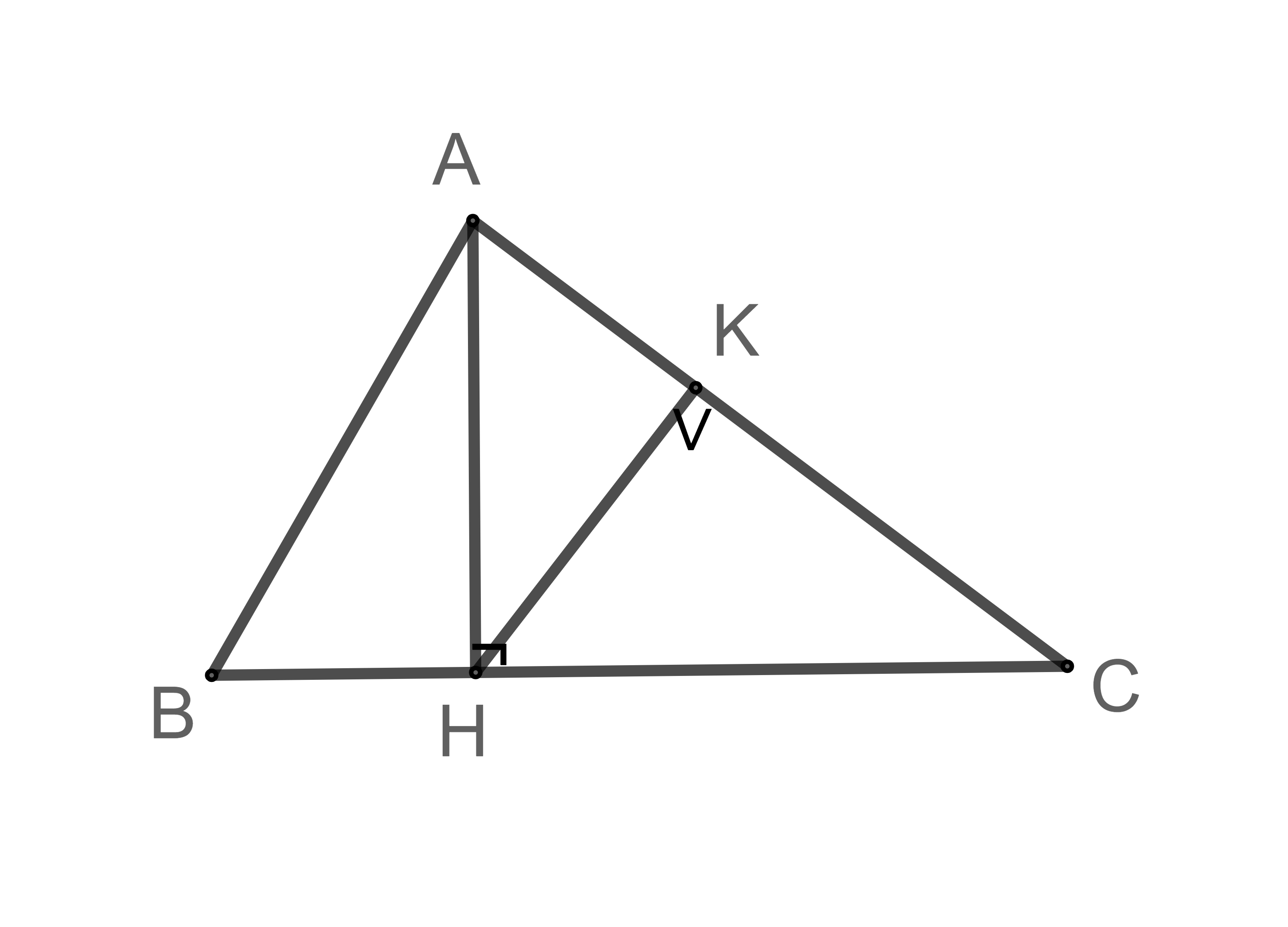
– = 90° (do cạnh vuông góc với mặt phẳng cùng nằm trên một mặt phẳng)
– là góc chung
– Suy ra: AHC ≈ HKC (đpcm)

2.2. Chứng minh tam giác đồng dạng để suy ra một tỉ số hay một biểu thức nào đó

Ví dụ: Cho tam giác ABC nhọn. Từ A kẻ AH vuông góc với BC (H BC), từ H kẻ HK vuông góc với AC (K AC). Chứng minh: KH^2 = KA.KC

Giải

Xét tam giác AHC và tam giác AKH có:

– = 90° (do cạnh vuông góc với mặt phẳng cùng nằm trên một mặt phẳng)
– là góc chung
– Suy ra: AHC ≈ AKH (c.g.c)
– Từ (1) và (2) suy ra: HKC ≈ AKH (vì cùng đồng dạng với tam giác AHC)
– Do đó, KH^2 = KA.KC (đpcm)

2.3. Các dạng bài khác liên quan đến chứng minh tam giác đồng dạng

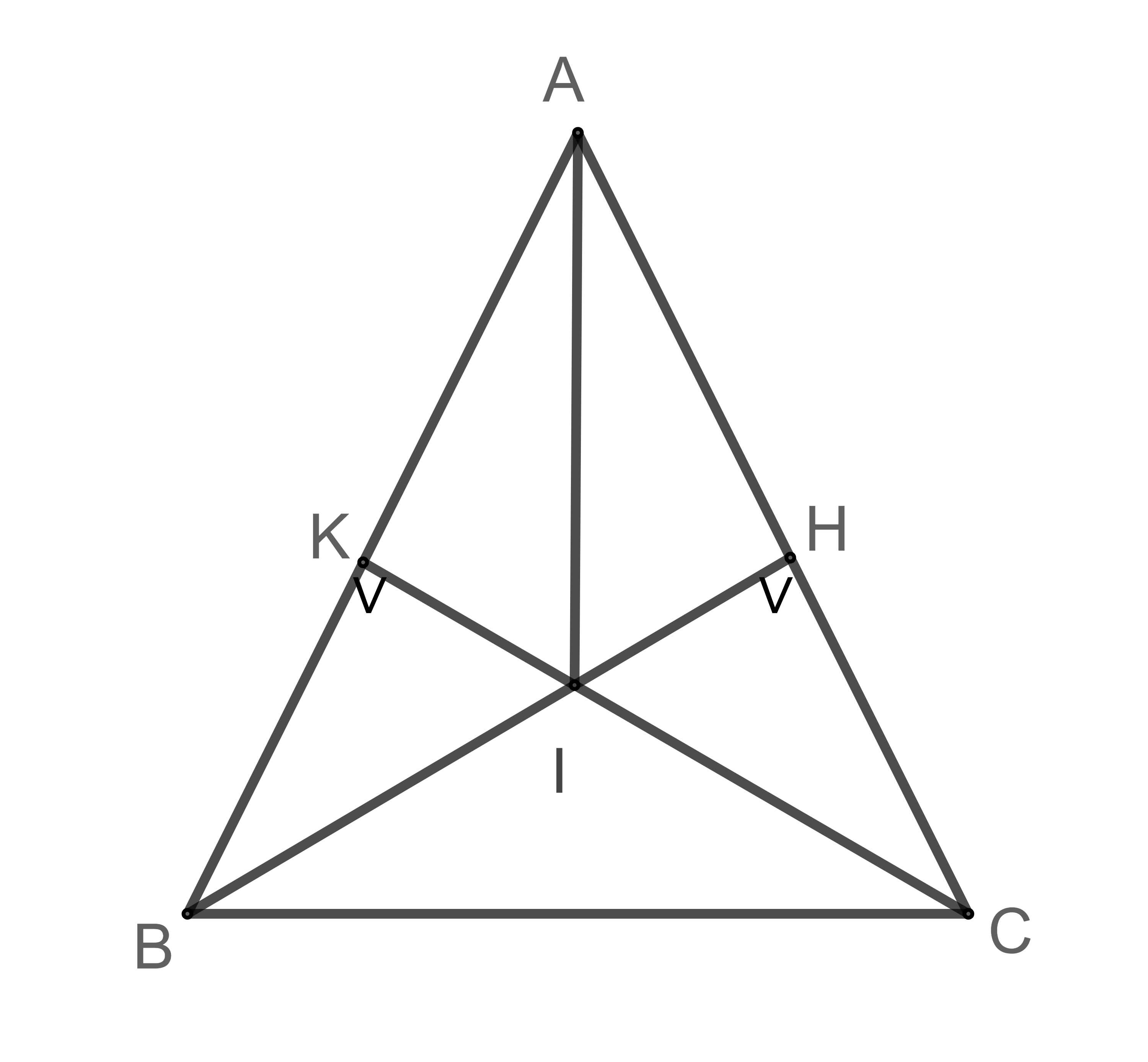
Ví dụ: Cho tam giác ABC cân tại A. Kẻ lần lượt các đường cao BH, CK (H AC, K AB). Gọi I là giao điểm của BH và CK.

a. Có thể kết luận tam giác BKC và tam giác CHB là hai tam giác đồng dạng hay không? Tìm tỉ số đồng dạng nếu có.

b. Chứng minh AI là đường phân giác của góc A.

Giải

• Xét tam giác BKC và tam giác CHB có:
• = 90° (do tam giác ABC cân tại A)
• Suy ra: BKC ≈ CHB
• Do đó, k = BC/CH = AB/BK = AC/CK = 1
• Vậy, tam giác BKC và tam giác CHB là hai tam giác đồng dạng theo tỉ số k = 1.

b. Vì tam giác BKC và tam giác CHB là hai tam giác đồng dạng theo tỉ số k = 1.

Nên BKC = CHB

Suy ra: BK = CH (cặp cạnh tương ứng)

Mà AB = AK + BK ; AC = AH + CH ; AB = AC

Nên AK = AH

• Xét hai tam giác vuông AKI và AHI có:

AK = AH (cmt)

AI là cạnh chung

Do đó, AKI = AHI (cạnh huyền – cạnh góc vuông)

Suy ra:

Vậy, AI là đường phân giác của góc A.

Bên cạnh các kiến thức lý thuyết và ví dụ minh họa về chứng minh tam giác đồng dạng, bạn có thể tham khảo thêm các cách chứng minh 2 tứ giác đồng dạng với nhau trong bài viết sau:

• Tổng hợp các cách chứng minh 2 tứ giác đồng dạng

Bài tập chứng minh tam giác đồng dạng lớp 8

Bài 1: Hai tam giác vuông đồng dạng với nhau khi:

• Có cạnh huyền bằng nhau
• Có một cạnh góc vuông bằng nhau
• Có một góc nhọn bằng nhau
• A, B, C đều đúng

ĐÁP ÁN
Chọn câu C

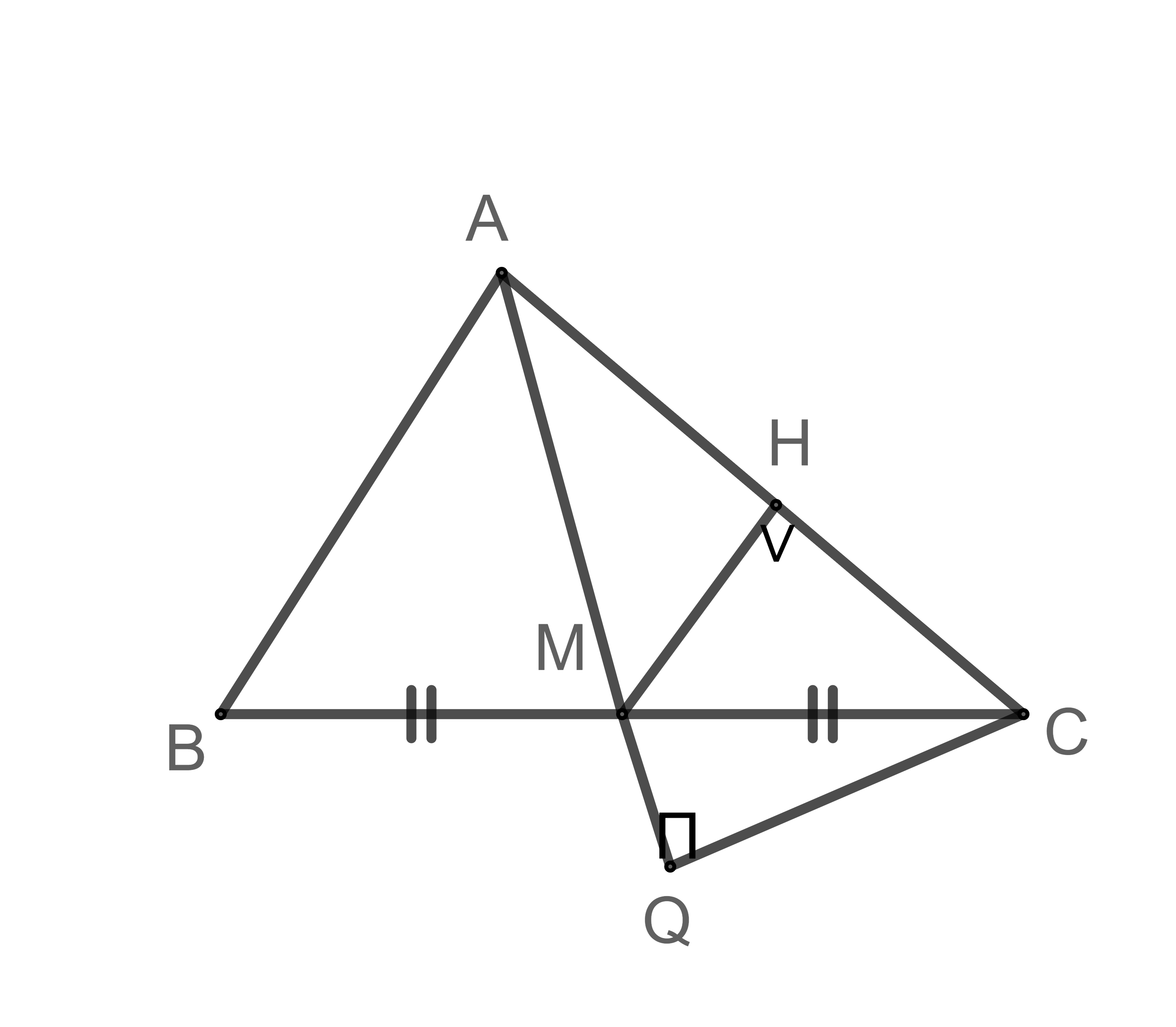
Bài 2: Cho tam giác nhọn ABC có AB < AC. Gọi M là trung điểm BC. Từ M, kẻ MH vuông góc với AC (H AC). Đường thẳng qua C và vuông góc với AM, cắt AM tại Q. Lúc này, số cặp tam giác đồng dạng với nhau là:

• Không có cặp nào
• 1 cặp
• 2 cặp
• 3 cặp

ĐÁP ÁN

Chỉ có 1 cặp tam giác đồng dạng với nhau là tam giác AQC và tam giác AHM

Chọn câu B

Bài 3: Cho tam giác nhọn ABC có AB < AC. Gọi M là trung điểm BC. Từ M, kẻ MH vuông góc với AC (H AC). Đường thẳng qua C và vuông góc với AM, cắt AM tại Q. Biết AQ = 4 cm; QC = 3 cm. Hãy cho biết trong các kết luận dưới đây, kết luận đúng là:

ĐÁP ÁN

• Xét tam giác AHM và tam giác AQC có:

• = 90°
• là góc chung
• Suy ra: AHM ≈ AQC
• Do đó,

Hay

• Áp dụng định lý Py-ta-go vào tam giác ACQ vuông tại Q ta có:
  AC^2 = AQ^2 + QC^2 = 4^2 + 3^2 = 25
  Vậy, AC = 5 cm
  Suy ra:

Chọn câu D

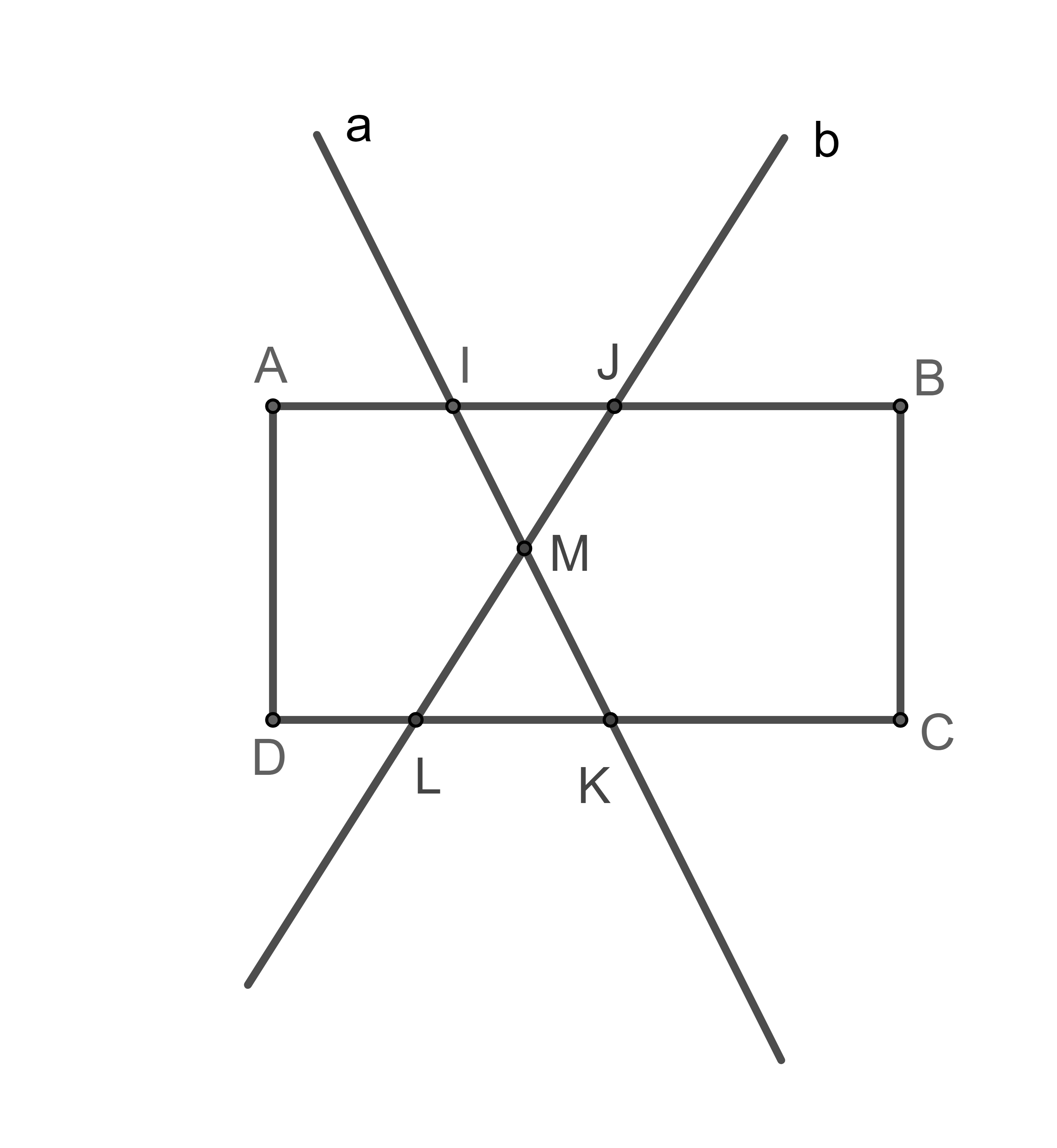
Bài 4: Cho hình chữ nhật ABCD. Đường thẳng a cắt AB, CD lần lượt tại I, K. Đường thẳng b cắt AB, CD lần lượt tại J, L. Biết đường thẳng a cắt đường thẳng b tại M. Biết IJ = x (cm) và LK = y (cm). Trong các phát biểu sau, phát biểu sai là:

• Trong hình vẽ nêu trên, chúng ta có thể tìm được một cặp tam giác đồng dạng theo trường hợp góc – góc

ĐÁP ÁN
Xét tam giác IMJ và tam giác KML có:

• đối đỉnh
• cặp góc so le trong, AB // CD
  Do đó, IMJ ≈ KML (g.g)
  Suy ra:
  Vậy, A, B, D đúng.

Chọn câu C

Bài 5: Trong tam giác vuông, trường hợp đồng dạng theo hai cạnh góc vuông ứng với trường hợp đồng dạng nào trong tam giác thường?

• Cạnh – cạnh – cạnh
• Cạnh – góc – cạnh
• Góc – góc
• Không thể kết luận

ĐÁP ÁN
Chọn câu B

Bài 6: Tam giác thứ nhất đồng dạng với tam giác thứ hai theo tỉ số đồng dạng k1 = 2, tam giác thứ hai đồng dạng với tam giác thứ ba theo tỉ số đồng dạng k2 = 4. Khi đó:

• Tam giác thứ nhất đồng dạng với tam giác thứ ba theo tỉ số đồng dạng k = 8
• Tam giác thứ nhất đồng dạng với tam giác thứ ba theo tỉ số đồng dạng k = 2
• Tam giác thứ nhất đồng dạng với tam giác thứ ba theo tỉ số đồng dạng k =
• Tam giác thứ nhất đồng dạng với tam giác thứ ba theo tỉ số đồng dạng k = 4

ĐÁP ÁN

• Giả sử theo k1 = 2
  Suy ra:
• Giả sử theo k2 = 4
  Suy ra:
• Lúc này,
  theo tỉ số k =
  Chọn câu A

Mong rằng qua bài viết này, các bạn đã nắm vững cách chứng minh đồng dạng của tam giác và có thể áp dụng vào các bài toán chứng minh tam giác đồng dạng.