Các dạng bài tập hàm số bậc nhất và lời giải chi tiết [Toán lớp 9]

Trong bài viết này, chúng ta sẽ tìm hiểu về các dạng toán về hàm số bậc nhất và cách giải chúng. Hãy cùng khám phá chi tiết qua các bài tập vận dụng có lời giải dưới đây.

Ôn tập kiến thức về hàm số bậc nhất

Định nghĩa hàm số bậc nhất

• Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a và b là các số cho trước và a khác 0. Đặc biệt, khi b = 0 thì hàm có dạng y = ax.

Tính chất hàm số bậc nhất

• Hàm số bậc nhất y = ax + b (a khác 0) xác định với mọi giá trị của x thuộc R và:
  • Đồng biến trên R khi a > 0.
  • Nghịch biến trên R khi a < 0.

Đồ thị của hàm số bậc nhất

• Đồ thị của hàm số y = ax + b (a khác 0) là một đường thẳng.
• Đồ thị cắt trục tung tại điểm có tung độ bằng b.
• Đồ thị song song với đường thẳng y = ax nếu b khác 0 và trùng với đường thẳng y = ax nếu b = 0.
• Số a gọi là hệ số góc, số b gọi là tung độ gốc của đường thẳng.

Góc tạo bởi đồ thị hàm số bậc nhất và trục Ox

• Gọi α là góc tạo bởi đường thẳng y = ax + b (a khác 0) và trục Ox.
• Nếu α > 0 thì tanα = a (góc tạo bởi hàm số và trục Ox là góc nhọn).
• Nếu α < 0 ta đặt β = 1800 – α, khi đó tanβ = |α| (góc tạo bởi hàm số và trục Ox là góc tù).
• Tính β rồi suy ra α = 1800 – β.

Vị trí tương đối của hai đường thẳng, đường thẳng và parabol

• Cho các đường thẳng (d): y = ax + b (a khác 0) và (d’): y = a’x + b’ (a’ khác 0) khi đó:
  • (d) X (d’) ⇔ a khác a’
  • (d) // (d’) ⇔ a = a’ và b khác b’
  • (d) ≡ (d’) ⇔ a = a’ và b = b’
  • (d) ⊥ (d’) ⇔ a * a’ = -1

Các dạng toán về hàm số bậc nhất

Dạng 1: Viết phương trình đường thẳng

Viết phương trình đường thẳng (d) đi qua điểm M(1;2) và có hệ số góc là 3.

Lời giải:

• Phương trình đường thẳng có hệ số góc 3 (tức a = 3) có phương trình dạng: y = 3x + b.
• Vì phương trình này đi qua điểm M(1;2) nên có: 2 = 3 * 1 + b ⇔ b = 2 – 3 ⇔ b = -1.
  Vậy phương trình đường thẳng cần tìm là: y = 3x – 1

Dạng 2: Xác định m để 2 đường thẳng cắt nhau

Cho đường thẳng (d1): y = -x + 2 và đường thẳng (d2): y = 2x + m – 3. Xác định m để (d1) cắt (d2) tại điểm nằm trên trục hoành.

Lời giải:

• Ta thấy (d1) luôn cắt (d2) vì a1 = -1 khác a2 = 2.
• Đường thẳng d1: y = -x + 2 cắt trục hoành (y = 0) nên có: 0 = -x + 2 ⇒ x = 2
  Vậy d1 cắt trục hoành tại điểm (2;0)
• Đường thẳng d2: y = 2x + m – 3 cắt trục hoành (y=0) nên có: 0 = 2x + m – 3 ⇒ 2x = -m + 3 ⇒ x = (-m + 3)/2
  Vậy d2 cắt trục hoành tại điểm
  ⇒ Để d1 cắt d2 tại một điểm trên trục hoành thì:

(-m+3)/2=2 <=> -m+3=4 <=> m=-1

Với m = -1 thì d2 có phương trình: y = 2x – 4.

Khi đó hai đường thẳng y = -x + 2 và đường thẳng y = 2x – 4 cắt nhau tại một điểm có tọa độ (2;0) nằm trên trục hoành.

Dạng 3: Xác định m để 2 hàm số biến thiên, song song hoặc đi qua 1 điểm

Cho các hàm số y = 2mx + m + 1 (1) và hàm số y = (m – 1)x + 3 (2)
a) Xác định m để hàm số (1) đồng biến, hàm số (2) nghịch biến.
b) Xác định m để đồ thị hàm số (1) song song với đồ thị hàm số (2)
c) Chứng minh rằng đồ thị (d) của hàm số (1) luôn đi qua 1 điểm cố định với mọi giá trị của m.

Lời giải:
a) Xác định m để hàm số (1) đồng biến, hàm số (2) nghịch biến.

• Hàm số (1) đồng biến (tức a > 0) ⇔ 2m > 0 ⇔ m > 0
• Hàm số (2) nghịch biến (tức a < 0) ⇔ m – 1 < 0 ⇔ m < 1
  ⇒ Để hàm số (1) đồng biến và hàm số (2) nghịch biến thì m thỏa: 0 < m < 1.

b) Xác định m để đồ thị hàm số (1) song song với đồ thị hàm số (2)

• Để đồ thị của hàm số (1) // (2) thì:

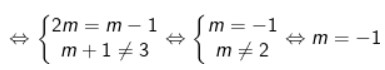
c) Chứng minh rằng đồ thị (d) của hàm số (1) luôn đi qua 1 điểm cố định với mọi giá trị của m.

• Viết lại hàm số (1) như sau: y = m(2x + 1) + 1, ta thấy:
  Với mọi giá trị của m, khi x = -1/2 thì y = 1.
  → Vậy đồ thị (d) của hàm số (1) luôn đi qua 1 điểm cố định là điểm M(-1/2; 1)

Dạng 4: Xác định m để hàm số cắt 2 trục, song song hoặc vuông góc với 1 đường thẳng

Cho hàm số y = (m – 3)x + m + 2 (1)
a) Tìm m để đồ thị (d) cắt trục tung tại điểm có tung độ bằng -3
b) Tìm m để đồ thị (d) song song với đường thẳng (d1): y = -2x + 1
c) Tìm m để đồ thị (d) vuông góc với đường thẳng (d2): y = 2x – 5

Lời giải:
a) Tìm m để đồ thị (d) cắt trục tung tại điểm có tung độ bằng -3
• Để đồ thị hàm số y = (m – 3)x + m + 2 cắt trục tung tại điểm có tung độ bằng -3, tức là x = 0; y = -3 nên có:

• 3 = (m – 3).0 + m + 2 ⇒ m = – 5.
  → Vậy với m = – 5 thì đồ thị hàm số (d) cắt trục tung tại điểm có tung độ bằng -3.

b) Tìm m để đồ thị (d) song song với đường thẳng (d1): y = -2x + 1.
• Để đồ thị hàm số (d): y = (m – 3)x + m + 2 song song với đường thẳng (d1): y = -2x + 1 thì:

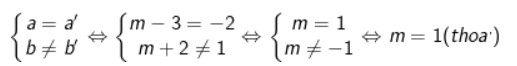
Với a’ là hệ số góc của (d1) b’ là tung độ góc của (d1).
→ Vậy với m = 1 thì đồ thị hàm số (d) // (d1): y = -2x + 1.

c) Tìm m để đồ thị (d) vuông góc với đường thẳng y = 2x – 5
• Để đồ thị hàm số (d): y = (m – 3)x + m + 2 vuông góc với đường thẳng y = 2x – 5 thì:

a.a’ = -1 <=> (m – 3).2 = -1 <=> 2m – 6 = – 1 <=> m = 5/2

Với a’ là hệ số góc của (d2).
→ Vậy với m = 5/2 thì đồ thị hàm số (d) ⊥ (d2): y = 2x – 5.

Dạng 5: Xác định m để hàm số đi qua 1 điểm hoặc cắt đồ thị hàm số khác

Cho hàm số y = 2x + m. (1)
a) Xác định giá trị của m để hàm số đi qua điểm A(-1;3)
b) Xác định m để đồ thị hàm số (1) cắt đồ thì hàm số y = 3x – 2 trong góc phần tư thứ IV.

Lời giải:
a) Để đồ thị hàm số y = 2x + m đi qua điểm A(-1;3) thì:
3 = 2.(-1) + m ⇔ m = 3 + 2 ⇔ m = 5.
Vậy mới m = 5 thì đồ thị hàm số y = 2x + m đi qua điểm A(-1;3).

b) Tọa độ giao điểm của đồ thị hàm số y = 2x + m với đồ thị hàm số y = 3x – 2 là nghiệm của hệ phương trình:

Dạng 6: Tính góc được tạo bởi đồ thị hàm số với 2 trục và tính diện tích của tam giác

Xác định hàm số y = ax + b biết đồ thị (d) của nó đi qua điểm A(4;0) và B(0;3). Khi đó hãy tính:
a) Vẽ đồ thị hàm số (d) vừa tìm được và tính góc α tạo bởi đường thẳng (d) và trục Ox.
b) Khoảng cách từ gốc tọa độ O đến đường thẳng (d)
c) Tính diện tích tam giác OAB

Lời giải:
a) Vì (d) đi qua 2 điểm A(4;0) và B(0;3) có đồ thị như sau:

Bài tập hàm số bậc nhất tự luyện

• Bài tập 1:
  Cho hàm số y = (2m + 1) + m + 4 có đồ thị là (d).
  a) Tìm m để (d) đi qua điểm A(-1;2)
  b) Tìm m để (d) song song với đường thẳng (d1) có phương trình y = 5x + 1
  c) Chứng minh rằng khi m thay đổi thì đường thẳng (d) luôn đi qua một điểm cố định.
• Bài tập 2:
  Cho hàm số y = (m + 5)x + 2m – 10
  a) Với giá trị nào của m thì y là hàm số bậc nhất
  b) Với giá trị nào của m thì hàm số đồng biến.
  c) Tìm m để đồ thị hàm số đi qua điểm A(2; 3)
  d) Tìm m để đồ thị cắt trục tung tại điểm có tung độ bằng 9.
  e) Tìm m để đồ thị đi qua điểm 10 trên trục hoành.
  f) Tìm m để đồ thị hàm số song song với đồ thị hàm số y = 2x – 1
  g) Chứng minh đồ thị hàm số luôn đi qua 1 điểm cố định với mọi m.
  h) Tìm m để khoảng cách từ O tới đồ thị hàm số là lớn nhất.

• Bài tập 3:
  Cho hàm số y = (2m – 3)x + m – 5
  a) Vẽ đồ thị hàm số với m = 2
  b) Chứng minh họ đường thẳng luôn đi qua điểm cố định khi m thay đổi
  c) Xác định m để đồ thị hàm số tạo với 2 trục toạ độ một tam giác vuông cân
  d) Xác định m để đồ thị hàm số tạo với trục hoành một góc 300
  e) Xác định m để đồ thị hàm số tạo với trục hoành một góc 1350
  f) Xác định m để đồ thị hàm số cắt đường thẳng y = 3x – 4 tại một điểm trên Oy
  g) Xác định m để đồ thị hàm số cắt đường thẳng y = -x – 3 tại một điểm trên Ox.