Bất Phương Trình Chứa Căn Lớp 10: Giải Nhanh Chóng và Hiệu Quả!

Hẳn các bạn học sinh lớp 10 đã từng gặp phải các bài toán bất phương trình chứa căn và cảm thấy khó khăn trong việc giải quyết chúng. Bài viết này sẽ giúp các bạn giải quyết những bài toán này một cách nhanh chóng và hiệu quả nhất.

Các Công Thức Giải Bất Phương Trình Chứa Căn

Chúng ta có thể sử dụng các công thức sau để giải bất phương trình chứa căn:

Công thức 1:

$$sqrt{f(x)} < g(x) Leftrightarrow left{begin{matrix}f(x) geq 0 g(x) geq 0 f(x) < g^{2}(x) end{matrix}right.$$

Hoặc nếu có dấu bằng, ta có:

$$sqrt{f(x)} leq g(x) Leftrightarrow left{begin{matrix}f(x) geq 0 g(x) geq 0 f(x) leq g^{2}(x) end{matrix}right.$$

Ví dụ: Giải bất phương trình: $sqrt{x}+sqrt{y-1}+sqrt{z-2}=frac{1}{2}(x+y+z)$

Giải:

Điều kiện: $x geq 0; y geq 1; z geq 2$

Phương trình tương đương:

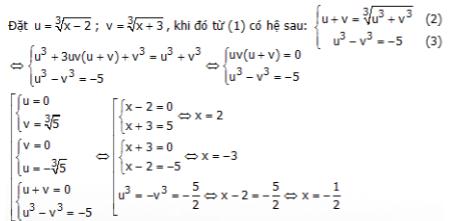
Công thức 2:

Hoặc trường hợp có thêm dấu bằng, ta có:

Ví dụ: Giải bất phương trình: $x^{2}+9x+20=2sqrt{3x+10}$

Điều kiện: $x leq frac{-10}{3}$

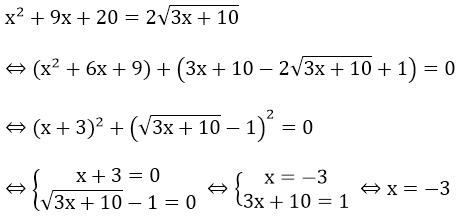
Nghiệm của bất phương trình là $x= -3$.

Đăng ký ngay để được các thầy cô ôn tập và xây dựng lộ trình học tập THPT vững vàng.

Một Số Cách Giải Chi Tiết Bất Phương Trình Chứa Căn Bậc Hai

2.1. Phương trình và bất phương trình chứa căn thức cơ bản

Ví dụ 1: Giải các bất phương trình sau:

$$sqrt{x^{2}-x-12}=7-x$$

Giải:

$$Rightarrow text{Nghiệm của phương trình là:} x=frac{61}{13}$$

Ví dụ 2: Tìm tập nghiệm của bất phương trình sau:

$$sqrt{x-3}<2x-1$$

Giải:

$$Rightarrow text{Nghiệm của bất phương trình } S=[3,infty)$$

2.2. Quy phương trình chứa căn thức về hệ phương trình không chứa căn thức

Chúng ta có thể sử dụng phương pháp đặt phụ để quy phương trình căn thức về hệ phương trình không chứa căn thức. Ta có ví dụ sau đây:

Ví dụ: Giải phương trình sau:

$$sqrt[3]{x-2}+sqrt[3]{x+3}=sqrt[3]{2x+1}$$

Giải:

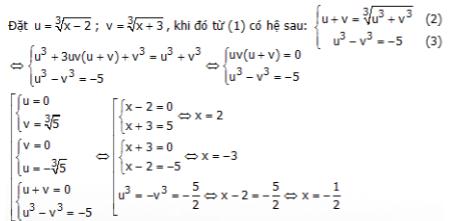
Vậy phương trình có các nghiệm $x=2$, $x=-3$ và $x=frac{-1}{2}$.

Ví dụ 2: Giải phương trình sau:

$$2(x^{2}+2)=5sqrt{x^{3}+1}$$

Giải:

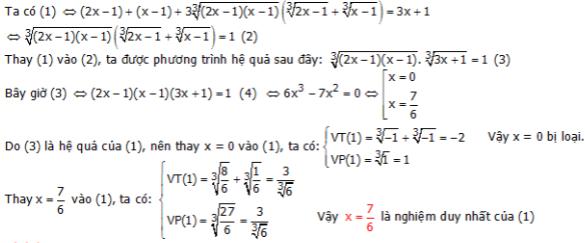
2.3. Sử dụng phương trình tương đương hoặc hệ quả

Ví dụ 1: Giải phương trình sau:

$$sqrt[3]{2x-1}+sqrt[3]{x-1}=sqrt[3]{3x+1}$$

Giải:

Ví dụ 2: Giải phương trình sau:

$$sqrt{2x+3}+sqrt{x+1}=3x+2sqrt{2x^{2}+5x+3}-16$$

Giải:

Đặt $u=sqrt{2x+3}+sqrt{x+1} geq 1$

Ta có $u^{2}=3x+4+2sqrt{2x^{2}+5x+3}$ với $ugeq 1$

Thay vào phương trình ban đầu, ta có phương trình hệ quả sau:

$$u^{2}-20=u Leftrightarrow u^{2}-u-20=0$$

$$Leftrightarrow u=5 text{ hoặc } u=-4 Leftrightarrow u=5 text{ (do } ugeq 0 text{)}$$

Từ đó, ta thay $x = 3$ vào phương trình ban đầu và nhận được kết quả chính xác, vậy phương trình ban đầu có nghiệm $x = 3$.

2.4. Sử dụng phương pháp chiều biến thiên hàm số

Ví dụ 1: Giải phương trình sau:

$$x^{5}+x^{3}-sqrt{1-3x}+4=0$$

Giải:

Đặt $f(x)=x^{5}+x^{3}-sqrt{1-3x}+4$ với $xleq frac{1}{3}$

Khi đó, phương trình có dạng $f(x) = 0$ và miền xác định $xleq frac{1}{3}$

Ta có $f'(x)=5x^{4}+3x^{2}+frac{3}{2sqrt{1-3x}}>0, forall x leq frac{1}{3}$

Vậy $f(x)$ là hàm số đồng biến khi $x<frac{1}{3}$

Ta có $f'(-1)=0$, vậy $x=-1$ là nghiệm duy nhất của phương trình.

Ví dụ 2: Giải phương trình:

$$sqrt{x^{2}+15}=3x-2+sqrt{x^{2}+8}$$

Giải:

Ta viết phương trình dưới dạng $f(x)=3x-2+sqrt{x^{2}+8}-sqrt{x^{2}+15}=0$

Hàm số $f(x)$ xác định với $forall x in R$. Xét phương trình với 2 khả năng sau:

$$Rightarrow x=1 text{ là nghiệm duy nhất của phương trình}$$

2.5. Phương pháp đánh giá hai vế

Với phương trình $f(x)=g(x)$, ta có tính chất:

$$f(x)geq A , forall x in D text{ hoặc } g(x)geq A , forall x in D$$

Khi đó: $f(x)=g(x) Leftrightarrow f(x)=A$ hoặc $g(x)=A$

Để bất đẳng thức $f(x)geq A; g(x)leq A; forall x in A$ ta áp dụng các kiến thức về bất đẳng thức.

Ví dụ 1: Giải phương trình sau:

$$sqrt{x-2}+sqrt{4-x}=x^{2}-6x+11$$

Giải:

Ta có miền xác định của phương trình là $D=left { {x:2leq x leq 4} right }$

Ta có $x^{2}-6x+11=(x-3)^{2}+2geq 2, forall x in D$ thì $f^{2}(x)=2+2sqrt{(x-2)(4-x)}leq 2+[(x-2)+(4-x)]=4$

Do đó $f(x)geq 0$ khi $forall x in D Rightarrow f(x)leq 2 , forall x, in D$

$$Rightarrow x^{2}-6x+11=2Leftrightarrow x=3$$

Hoặc $sqrt{x-2}+sqrt{4-x}Leftrightarrow x-2=4-x Leftrightarrow x=3$

$$Rightarrow x=3 text{ là nghiệm duy nhất của phương trình}$$

Ví dụ 2: Giải phương trình:

$$sqrt{3x^{2}+6x+7}+sqrt{5x^{2}+10x+14}=4-2x-x^{2}$$

2.6. Bất phương trình chứa căn thức có tham số

Ví dụ 1: Giải phương trình:

$$sqrt{x-4a+16}+2sqrt{x-2a+4}+sqrt{x}=0$$

Ví dụ 2: Giải và biện luận phương trình:

$$sqrt{x^{2}+x+frac{m^{2}}{(x-1)^{2}}}=x-frac{m}{x-1}$$

Nguồn: https://kienthuconline24h.com/