Tam giác vuông là một trong những dạng hình học quan trọng trong toán học. Trong bài viết này, chúng ta sẽ tìm hiểu về các trường hợp tam giác vuông bằng nhau và cách giải chúng.
Tóm tắt
Các trường hợp tam giác vuông bằng nhau
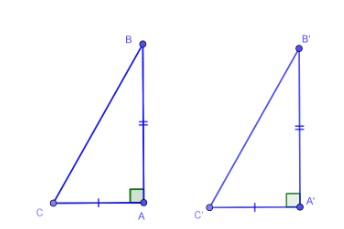
Hai cạnh góc vuông (hay là trường hợp cạnh – góc – cạnh).
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
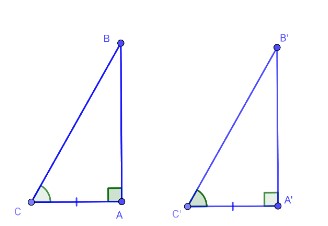
Cạnh góc vuông và góc nhọn kề với cạnh đó (hay là trường hợp góc – cạnh – góc)
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
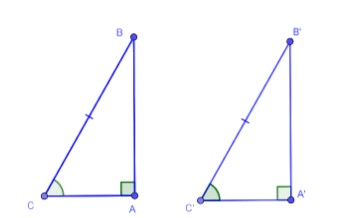
Cạnh huyền và góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (góc – cạnh – góc).
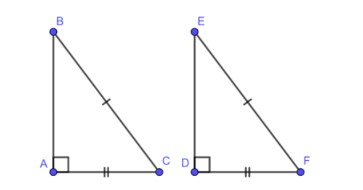
Trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Sau khi đã nắm rõ kiến thức về các trường hợp 2 tam giác vuông bằng nhau, hãy vận dụng vào làm các bài tập chứng minh nó. Bạn có thể tham khảo kiến thức và dạng bài tập này trong bài viết sau nhé:
- Cách chứng minh 2 tam giác vuông bằng nhau và bài tập vận dụng chi tiết
Bài tập cơ bản về hai tam giác vuông bằng nhau
Dạng 1: Chứng minh hai tam giác vuông bằng nhau
Phương pháp giải:
- Xét hai tam giác vuông.
- Kiểm tra điều kiện bằng nhau của hai tam giác: cạnh – góc – cạnh, góc – cạnh – góc, cạnh huyền – góc nhọn hoặc cạnh huyền – cạnh góc vuông.
- Kết luận hai tam giác bằng nhau.
Ví dụ minh họa: Cho ΔABC, BE và CD là đường cao của ΔABC. Chứng minh rằng:
ΔBCD=ΔCBE, biết BD = EC.
Giải:
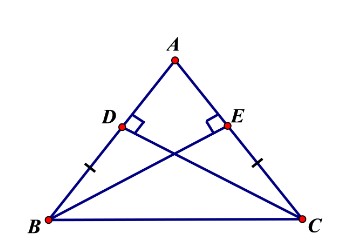
Xét ΔBCDvuông tại D và ΔCBE vuông tại E có:
BD = CE (gt)
Cạnh BC chung.
Nên ΔBCD=ΔCBE (cạnh huyền – cạnh góc vuông) (đpcm)
Ngoài ra, bạn có thể tìm hiểu các cách chứng minh 2 tam giác bất kỳ bằng nhau. Hãy tham khảo kiến thức này trong bài viết dưới đây nhé:
- [Chi tiết] Cách chứng minh tam giác bằng nhau đúng, chuẩn nhất
Dạng 2: Vận dụng hai tam giác bằng nhau để chứng minh đoạn thẳng, góc bằng nhau
Phương pháp giải:
- Chọn hai tam giác vuông có cạnh (góc) và hai đoạn (góc) cần chứng minh bằng nhau.
- Tìm thêm hai điều kiện bằng nhau, trong đó có một điều kiện về cạnh để kết luận hai tam giác bằng nhau.
- Suy ra hai cạnh (góc) tương ứng bằng nhau.
Ví dụ minh họa: Các tam giác ABC cân tại A (A^<90o). Vẽ BH⊥AC (H∈AC), CK⊥AB (K∈AB).
a) Chứng minh rằng AH = AK.
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng tia AI là tia phân giác của BAC^.
Giải:
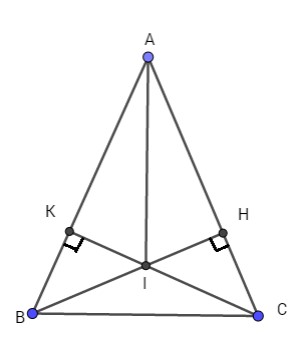
a) Xét ΔABH vuông tại H và ΔACK vuông tại K có:
AB = AC (ΔABC cân tại A)
A^ chung.
Nên ∆ABH = ∆ACK (cạnh huyền – góc nhọn)
⇒ AH = AK (hai cạnh tương ứng)
b) Xét ΔAIH vuông tại H và ΔAIK vuông tại K có:
AK = AH (cmt)
AI cạnh chung
Nên ∆AIK = ∆AIH (cạnh huyền – cạnh góc vuông)
⇒IAK^=IAH^ (hai góc tương ứng)
Vậy AI là tia phân giác của BAC^.
Dạng 3: Bổ sung thêm điều kiện để hai tam giác vuông bằng nhau
Phương pháp giải:
- Xét xem hai tam giác vuông đã có các yếu tố nào bằng nhau.
- Xét xem cần bổ sung thêm điều kiện nào để hai tam giác bằng nhau (dựa vào các trường hợp bằng nhau của hai tam giác).
Ví dụ minh họa: Các tam giác ABC và MNP có A^=M^=90o, B^=N^. Hãy bổ sung thêm một điều kiện bằng nhau để ∆ABC = ∆MNP.
Giải:
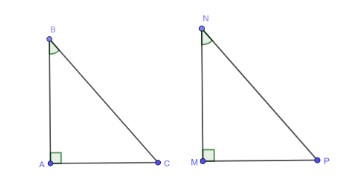
- Trường hợp 1: ΔABC = ΔMNP theo trường hợp cạnh góc vuông – góc nhọn kề.
Xét hai tam giác vuông ABC và MNP có:
B^=N^ (giả thiết)
Bổ sung AB = MN thì ΔABC = ΔMNP (cạnh góc vuông – góc nhọn kề). - Trường hợp 2: ΔABC = ΔMNP theo trường hợp hai cạnh huyền – góc nhọn.
Xét hai tam giác vuông ABC và MNP có:
B^=N^ (giả thiết)
Bổ sung BC = NP thì ΔABC = ΔMNP (cạnh huyền – góc nhọn).
Đến đây, chúng ta đã tìm hiểu về các trường hợp tam giác vuông bằng nhau và cách giải chúng. Các bạn có thể áp dụng kiến thức này để giải các bài tập toán lớp 7 có liên quan.


![[Tổng Hợp] Các cách chứng minh hình thoi cực chi tiết, dễ hiểu [Tổng Hợp] Các cách chứng minh hình thoi cực chi tiết, dễ hiểu](https://kienthuconline24h.com/wp-content/uploads/2024/01/cach-chung-minh-hinh-thoi-218x150.jpg)
![[Tổng Hợp] Các cách tính diện tích tam giác đầy đủ, chi tiết](https://kienthuconline24h.com/wp-content/uploads/2023/12/cac-cach-tinh-dien-tich-tam-giac-218x150.jpg)
