Tổng hợp các phương pháp chứng minh 2 tam giác bằng nhau

Hai tam giác bằng nhau là một khái niệm quan trọng trong môn Toán lớp 7. Bài viết này sẽ giúp bạn hiểu rõ về lý thuyết và cách chứng minh tam giác bằng nhau.

Thế nào là hai tam giác bằng nhau?

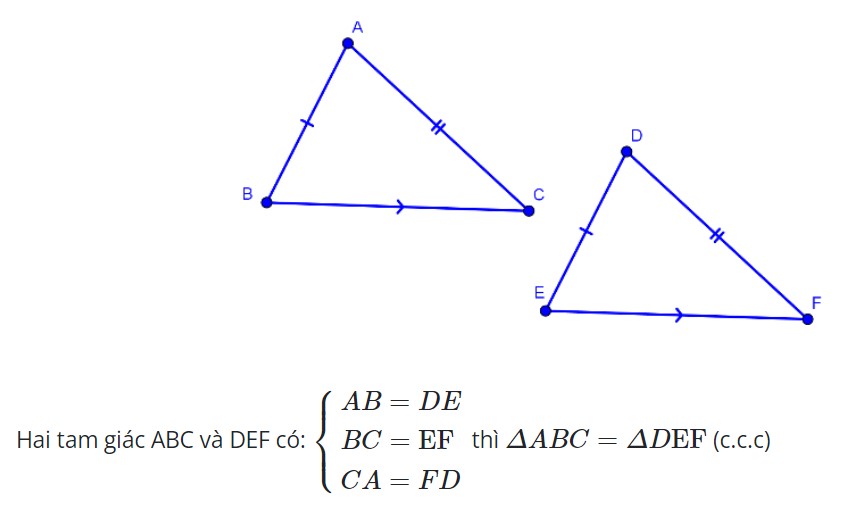
Hai tam giác ABC và A’B’C’ được coi là bằng nhau nếu các cạnh tương ứng của chúng bằng nhau và các góc tương ứng cũng bằng nhau. Điều này được biểu thị bằng các công thức sau:

• AB = A’B’
• AC = A’C’
• BC = B’C’
• A^=A’^
• B^=B’^
• C^=C’^

Để kí hiệu hai tam giác bằng nhau, chúng ta cần viết các đỉnh tương ứng theo cùng một thứ tự. Điểm A và A’ (B và B’, C và C’) là các đỉnh tương ứng; góc A và A’ (B và B’, C và C’) là các góc tương ứng; cạnh AB và A’B’ (AC và A’C’, BC và B’C’) là các cạnh tương ứng. Khi đó, chúng ta kí hiệu: ΔABC=ΔA’B’C’

Ví dụ, trong hình dưới đây, ta có:

• A^=H^=50°; B^=D^=23°; C^=E^=107° (các góc tương ứng)
• AB = DH = 5 cm; BC = DE = 4cm; AC = EH = 2cm (các cạnh tương ứng)

Do đó, hai tam giác trên bằng nhau. Kí hiệu theo thứ tự tương ứng là: ΔABC=ΔHDE

Cách chứng minh tam giác bằng nhau

Trường hợp bằng nhau thứ nhất của tam giác: Cạnh – cạnh – cạnh (c.c.c)

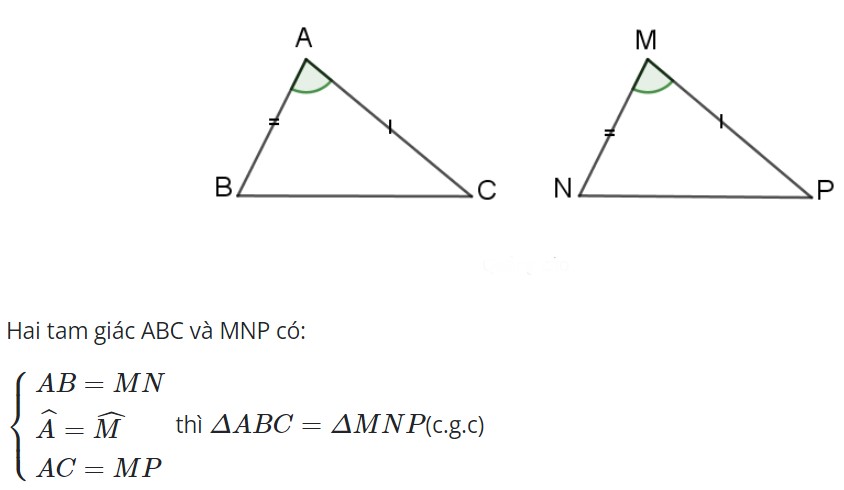
Trường hợp bằng nhau thứ 2 của tam giác: Cạnh – Góc – Cạnh

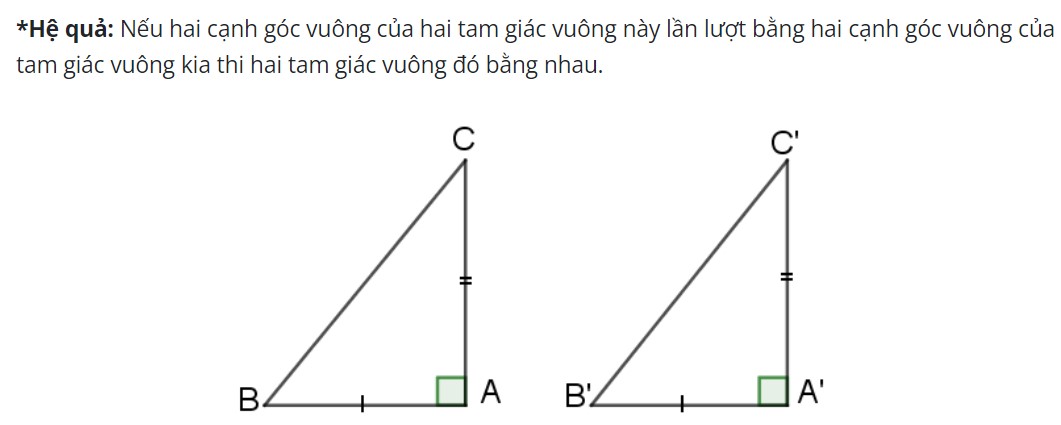
Đối với tam giác vuông, bạn có thể tham khảo thêm các trường hợp 2 tam giác vuông bằng nhau, từ đó có thể áp dụng cho bài chứng minh một cách dễ dàng. Bạn có thể tìm hiểu kiến thức này trong bài viết dưới đây:

• [Chi tiết] Các trường hợp tam giác vuông bằng nhau 

Trường hợp bằng nhau thứ 3 của tam giác: Góc – Cạnh – Góc

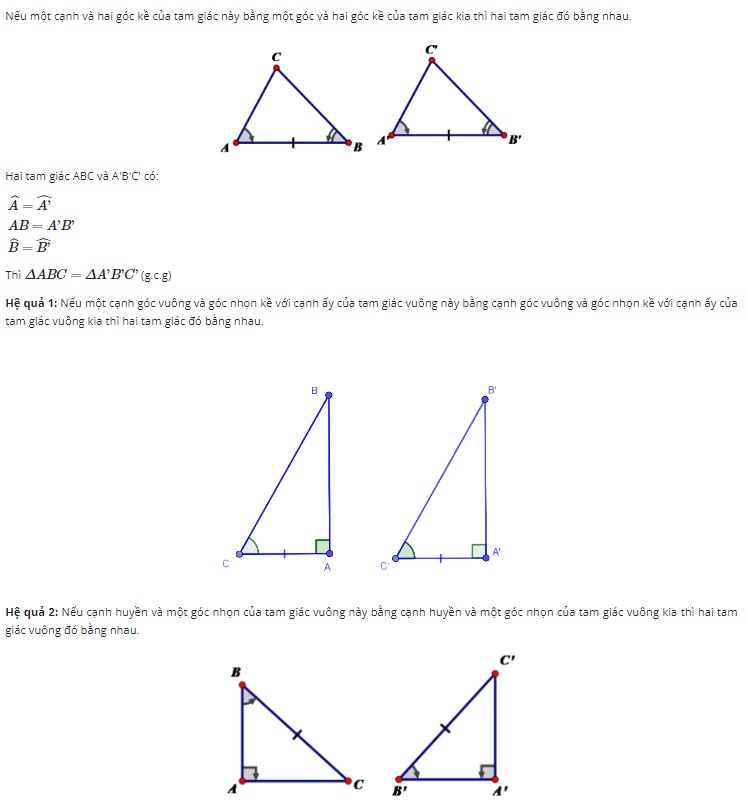
Tam giác vuông cũng là một trong các loại hình tam giác đặc biệt. Do đó, bạn có thể tìm hiểu các kiến thức và làm bài tập chứng minh 2 tam giác vuông bằng nhau. Xem ngay bài viết sau để bổ sung thêm kiến thức cho mình nhé:

• Tổng hợp các cách chứng minh tam giác vuông bằng nhau

Bài tập về hai tam giác bằng nhau

Bài 1: Cho tam giác ABC và DEH trong hình dưới đây. Xác định trong các khẳng định sau, khẳng định nào đúng?
a) ΔABC=ΔDEH;
b) ΔABC=ΔHDE;
c) ΔBAC=ΔDEH;
d) ΔBCA=ΔDEH.

Hướng dẫn giải:

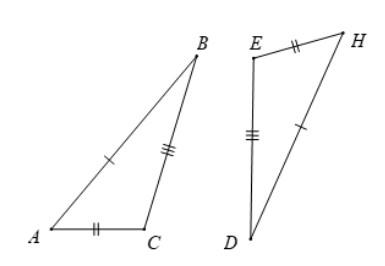
Hai tam giác ABC và HDE có:

• AB = HD
• BC = DE
• AC = HE

Vậy ΔABC=ΔHDE(c.c.c)

Khi đó A và H (B và D; C và E) là hai đỉnh tương ứng.

a) ΔABC=ΔDEH

Các đỉnh tương ứng không viết cùng thứ tự nên khẳng định sai.

b) ΔABC=ΔHDE

Các đỉnh tương ứng được viết cùng thứ tự nên khẳng định đúng.

c) ΔBAC=ΔDEH

Đỉnh A và H; đỉnh C và E không được viết cùng thứ tự nên khẳng định sai.

d) ΔBCA=ΔDEH

Các đỉnh tương ứng được viết cùng thứ tự nên khẳng định đúng.

Bài 2: Cho hình vẽ dưới đây, biết AD = BC, AC = BD. Chứng minh rằng ΔADB=ΔBCA.

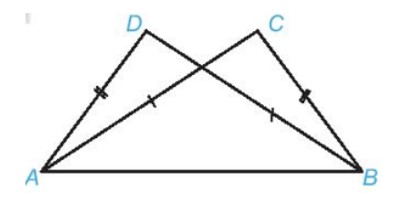
Hướng dẫn giải

Hai tam giác ADB và BCA có:

• AD = BC (theo giả thiết)
• BD = AC (theo giả thiết)
• AB là cạnh chung

Vậy ΔADB=ΔBCA(c.c.c)

Bài 3: Cho hình vẽ dưới đây, biết JG = JL, GK = LK, KJL^=60°, JGK^=90°.

a) Chứng minh rằng ΔJGK=ΔJLK

b) Tính góc GKL.

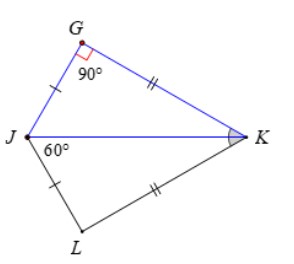
Hướng dẫn giải

a) Xét hai tam giác JGK và JLK có:

• JG = JL (theo giả thiết)
• GK = LK (theo giả thiết)
• JK là cạnh chung

Vậy ΔJGK=ΔJLK(c.c.c)

b) Vì ΔJGK=ΔJLK(theo câu a)

⇒ KJG^=KJL^(hai góc tương ứng)

⇒ KJG^=60°

Xét tam giác JGK có: KJG^+JGK^+GKJ^=180° (tổng 3 góc trong tam giác)

⇒ 60°+90°+GKJ^=180°

⇒ GKJ^=180°−60°−90°=30°

Vì ΔJGK=ΔJLK(theo câu a)

⇒ GKJ^=LKJ^(hai góc tương ứng)

⇒ GKL^=GKJ^+LKJ^=GKJ^+GKJ^=2GKJ^=2⋅30°=60°

Vậy GKL^=60°

Nếu bạn cần tìm hiểu thêm về các lý thuyết toán khác, hãy ghé thăm kienthuconline24h.com để cập nhật những bài viết hấp dẫn và chi tiết nhé.