Chào các bạn! Trong bài viết này, chúng ta sẽ cùng tìm hiểu về các cách chứng minh hình thoi một cách chi tiết và dễ hiểu nhé.
Tóm tắt
1. Nhắc lại về định nghĩa và tính chất của hình thoi
1.1. Định nghĩa hình thoi
- Hình thoi là một tứ giác có 4 cạnh bằng nhau.
Ví dụ: MNPQ là hình thoi khi và chỉ khi: MN = NP = PQ = QM
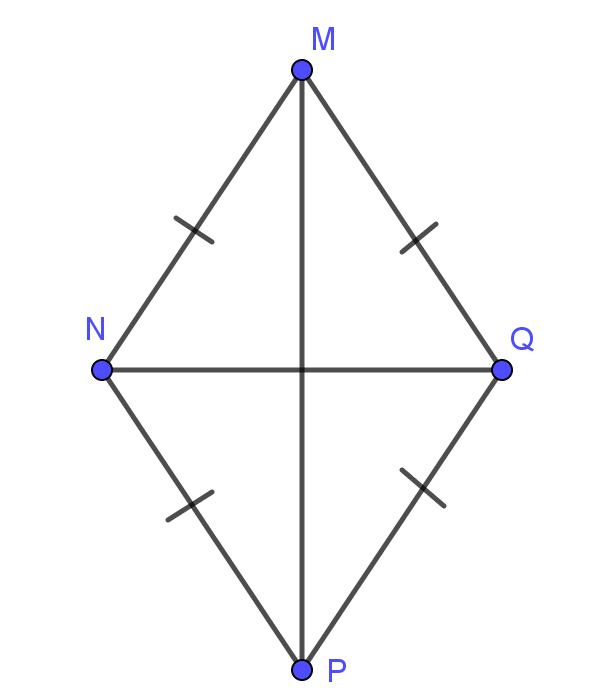
- Nếu một hình bình hành có hai cạnh kề bằng nhau hoặc hai đường chéo vuông góc với nhau thì đó là hình thoi.
Ví dụ: Cho MNPQ là hình bình hành. MNPQ trở thành hình thoi nếu:
- MN = NP hoặc NP = PQ hoặc PQ = QM
- Hoặc
1.2. Các tính chất của hình thoi
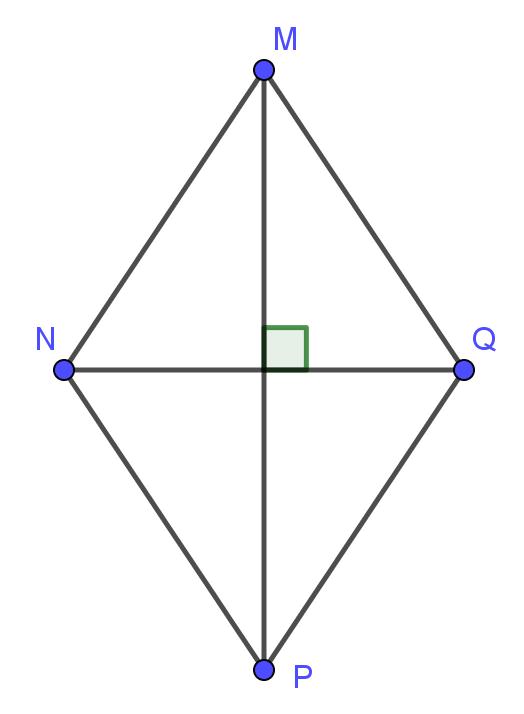
- Hình thoi có tất cả các tính chất của hình bình hành
- Hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường
- Hai đường chéo là các đường phân giác của các góc trong hình thoi
2. Cách chứng minh hình thoi
Dựa vào định nghĩa và tính chất của hình thoi, ta có các cách chứng minh hình thoi như sau:
- Cách 1: Chứng minh 4 cạnh của một tứ giác bằng nhau
Ví dụ: Để chứng minh tứ giác MNPQ là một hình thoi thì ta sẽ đi chứng minh:
MN = NP = PQ = QM - Cách 2: Chứng minh một tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường
Ví dụ: Muốn chứng minh tứ giác MNPQ là một hình thoi thì ta sẽ đi chứng minh:
Gọi I là trung điểm của MP và NQ thì: tại I - Cách 3: Chứng minh một tứ giác là hình bình hành có hai cạnh kề bằng nhau
Ví dụ: Nếu MNPQ là hình bình hành thì để chứng minh MNPQ cũng là hình thoi thì ta sẽ đi chứng minh:
MN = NP hoặc NP = PQ hoặc PQ = QM - Cách 4: Chứng minh hình bình hành có một đường chéo là phân giác của một góc
Ví dụ: Nếu MNPQ là hình bình hành thì để chứng minh MNPQ cũng là hình thoi thì ta sẽ đi chứng minh:
NQ là phân giác của góc MNP hoặc góc MQP
MP là phân giác của của góc NPQ hoặc góc NMQ - Cách 5: Chứng minh hình bình hành có hai đường chéo vuông góc với nhau
Ví dụ: Nếu MNPQ là hình bình hành thì để chứng minh MNPQ cũng là hình thoi thì ta sẽ đi chứng minh:
3. Các dạng bài tập về chứng minh hình thoi lớp 8
3.1. Dạng 1: Câu hỏi trắc nghiệm củng cố lý thuyết
- Câu 1: Tứ giác MNPQ là hình thoi khi và chỉ khi:
A. MN = MP = PQ = NQ
B. MN = NQ = PQ = QM
C. MN = NP = PQ = QM
D. MN = NP = PQ = MP
ĐÁP ÁN: Dựa vào định nghĩa, ta chọn đáp án đúng là C - Câu 2: Một hình bình hành là hình thoi khi:
A. Có hai đường chéo bằng nhau
B. Có hai đường chéo vuông góc với nhau
C. Hai đường chéo cắt nhau tại trung điểm mỗi đường
D. Hai cạnh đối bằng nhau
ĐÁP ÁN: Dựa vào các cách chứng minh, ta chọn đáp án đúng là B - Câu 3: Một tứ giác là hình thoi khi:
A. Hai đường chéo vuông góc với nhau
B. Hai đường chéo bằng nhau
C. Hai đường chéo cắt nhau tại trung điểm mỗi đường
D. Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường
ĐÁP ÁN: Dựa vào các cách chứng minh, ta chọn đáp án đúng là D - Câu 4: Một hình bình hành là hình thoi khi:
A. Hai cạnh kề bằng nhau
B. Hai cạnh đối bằng nhau
C. Hai cạnh đối song song với nhau
D. Hai cạnh đối song song và bằng nhau
ĐÁP ÁN: Dựa vào định nghĩa và các cách chứng minh, ta chọn đáp án đúng là A - Câu 5: Chọn đáp án sai. Hình bình hành là hình thoi khi
A. Hai đường chéo vuông góc với nhau
B. Một đường chéo là phân giác của một góc
C. Hai đường chéo bằng nhau
D. Một đường chéo vuông góc với đường chéo còn lại
ĐÁP ÁN: Dựa vào tính chất và cách chứng minh, ta chọn đáp án C
3.2. Dạng 2: Chứng minh một tứ giác là hình thoi
- Bài 1: Cho tứ giác MNPQ có MN // PQ, MN = NP = PQ.
a) Chứng minh MNPQ là hình bình hành
b) Chứng minh MNPQ là hình thoi
ĐÁP ÁN: a) Chứng minh MNPQ là hình bình hành
Xét tứ giác MNPQ có
- MN // PQ
- MN = PQ
⇒ MNPQ là hình bình hành (theo dấu hiệu nhận biết)
b) Chứng minh MNPQ là hình thoi
Theo a), MNPQ là hình bình hành
mà MN = NP
⇒ MNPQ là hình thoi (theo cách chứng minh 1)
- Bài 2: Cho tam giác MNQ cân tại M, có đường cao MA. Lấy điểm P đối xứng với M qua A. Chứng minh rằng:
a) NA = AQ
b) MNPQ là hình thoi
ĐÁP ÁN: a) Chứng minh NA = AQ
Ta có: Tam giác MNQ cân tại M
⇒ MA là đường cao đồng thời là đường trung tuyến
⇒ NA = AQ (đpcm)
b) Chứng minh rằng: MNPQ là hình thoi
hay (1)
P đối xứng với M qua A ⇒ A là trung điểm của MP
MA là đường trung tuyến trong tam giác MNQ ⇒ A là trung điểm của NQ
Mà MP và NQ cắt nhau tại A ⇒ MP, NQ cắt nhau tại trung điểm mỗi đường (2)
Từ (1) và (2) ⇒ MNPQ là hình thoi (theo cách chứng minh 2) - Bài 3: Cho tam giác MHK có MH = MK, đường trung tuyến MP, từ P kẻ PQ song song với MH (Q thuộc MK); kẻ PN song song với MK (N thuộc MH).
a) Chứng minh MNPQ là hình bình hành
b) Hình bình hành MNPQ là hình thoi
ĐÁP ÁN: a) Chứng minh MNPQ là hình bình hành
Ta có:
PQ // MH hay PQ // MN (1)
PN // MK hay PN // MQ (2)
Từ (1) và (2) ⇒ MNPQ là hình bình hành
b) Hình bình hành MNPQ là hình thoi
Ta có: MH = MK ⇒ Tam giác MHK cân tại M
⇒ Đường trung tuyến MP đồng thời là đường phân giác
Hình bình hành MNPQ có đường chéo MP là tia phân giác của góc NMQ
⇒ MNPQ là hình thoi
Từ đây, chúng ta đã tìm hiểu cách chứng minh hình thoi một cách chi tiết và dễ hiểu. Hy vọng những kiến thức này sẽ giúp các bạn trong quá trình học tập và làm bài tập. Nếu có bất kỳ thắc mắc nào, hãy liên hệ với chúng tôi để được giải đáp.
Nguồn: https://kienthuconline24h.com/
